II Design adaptations made in my design
This reasoning lets us work out how a relatively simple trebuchet would work but my trebuchet has two extra details in the construction. The first is the sling which is present on most trebuchets.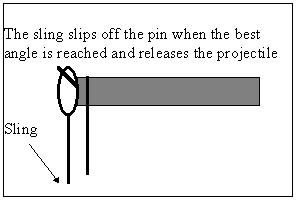 This sling changes slightly the working of the trebuchet however analysis of its motion is much more complex I will therefore not write about its working in detail. The sling is accelerated by the arm and increases the length of the projectile arm without adding much inertia to the trebuchet, thus allowing greater range. The sling is constantly in acceleration. I bent the pin such that it releases the sling when the optimal angle is reached.
This sling changes slightly the working of the trebuchet however analysis of its motion is much more complex I will therefore not write about its working in detail. The sling is accelerated by the arm and increases the length of the projectile arm without adding much inertia to the trebuchet, thus allowing greater range. The sling is constantly in acceleration. I bent the pin such that it releases the sling when the optimal angle is reached.
The second feature of the design of my trebuchet is the wheel from which the counterweight is suspended. A hanging counterweight is the limit of this idea, with a wheel of radius 0 at the very end of the counterweight arm. Having this wheel with a radius as big as the length of the counterweight arm greatly improves the efficiency of the counterweight. It falls straight down, with no sidewards movement, thus wasting minimal energy on sideways movement. All the force is normal to the wheel at every position of the arm. This counterweight creates a tension on the string which pulls the trebuchet. The force from the counterweight is always applied to the same point, with the same angle,
 and thus the counterweight can be omitted when calculating the moment of inertia of the trebuchet arm, greatly decreasing the moment of inertia allowing a greater angular acceleration with the same forces. The wheel from which the counterweight hangs does however have a moment of inertia which must be added to the moment of inertia. The inertia is
and thus the counterweight can be omitted when calculating the moment of inertia of the trebuchet arm, greatly decreasing the moment of inertia allowing a greater angular acceleration with the same forces. The wheel from which the counterweight hangs does however have a moment of inertia which must be added to the moment of inertia. The inertia is  . This is equal to
. This is equal to  because r is constant (assuming the spokes weigh nothing) and that in turn is equal to mr2 because the sum of the mass of all the points on the wheel is the mass of the whole wheel.
because r is constant (assuming the spokes weigh nothing) and that in turn is equal to mr2 because the sum of the mass of all the points on the wheel is the mass of the whole wheel.
Iwheel=mwheel×rwheel2
An interesting question is where to connect the string to the arm. The best spot is such that the string is perpendicular to it, and so there is no wasted force. If the string is at an angle, there is a force wasted as shown on diagram above. Another possible point to attach the string is to the rim of the circle.
BackNextHome
© Filip Radlinski 1996, 1997
 This sling changes slightly the working of the trebuchet however analysis of its motion is much more complex I will therefore not write about its working in detail. The sling is accelerated by the arm and increases the length of the projectile arm without adding much inertia to the trebuchet, thus allowing greater range. The sling is constantly in acceleration. I bent the pin such that it releases the sling when the optimal angle is reached.
This sling changes slightly the working of the trebuchet however analysis of its motion is much more complex I will therefore not write about its working in detail. The sling is accelerated by the arm and increases the length of the projectile arm without adding much inertia to the trebuchet, thus allowing greater range. The sling is constantly in acceleration. I bent the pin such that it releases the sling when the optimal angle is reached. and thus the counterweight can be omitted when calculating the moment of inertia of the trebuchet arm, greatly decreasing the moment of inertia allowing a greater angular acceleration with the same forces. The wheel from which the counterweight hangs does however have a moment of inertia which must be added to the moment of inertia. The inertia is
and thus the counterweight can be omitted when calculating the moment of inertia of the trebuchet arm, greatly decreasing the moment of inertia allowing a greater angular acceleration with the same forces. The wheel from which the counterweight hangs does however have a moment of inertia which must be added to the moment of inertia. The inertia is  . This is equal to
. This is equal to  because r is constant (assuming the spokes weigh nothing) and that in turn is equal to mr2 because the sum of the mass of all the points on the wheel is the mass of the whole wheel.
because r is constant (assuming the spokes weigh nothing) and that in turn is equal to mr2 because the sum of the mass of all the points on the wheel is the mass of the whole wheel.