The trebuchet is similar to a first order lever, with the counterweight providing the effort, the projectile supplying the load, and all of this is on a fulcrum. However, this is where the comparison ends, for the trebuchet is not trying to lift a load but to throw one.
Newton's second law of motion states:  . This is for a mathematical point motion but a similar formula is used for rotational rigid body motion.
. This is for a mathematical point motion but a similar formula is used for rotational rigid body motion.
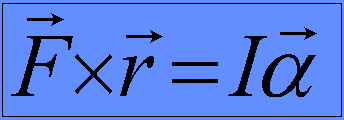 This formula is the shown on the right.
This formula is the shown on the right.  is acceleration but of the rotational type. It is called angular acceleration and is measured in radians per second squared. I is a function of the mass yet calculating it is slightly more complicated than calculating the total mass with translation motion. The exact formula is shown below. The name for I is moment of inertia. The given formula means that you cut whatever is accelerating into an infinite number of points, calculate the mass of each one multiplied by the distance from this point to the centre of rotation squared, and take
is acceleration but of the rotational type. It is called angular acceleration and is measured in radians per second squared. I is a function of the mass yet calculating it is slightly more complicated than calculating the total mass with translation motion. The exact formula is shown below. The name for I is moment of inertia. The given formula means that you cut whatever is accelerating into an infinite number of points, calculate the mass of each one multiplied by the distance from this point to the centre of rotation squared, and take  the sum of this for all the points. Luckily there is an easier way to go about it. The trebuchet arm is essentially made up of three different parts - the arm, the counterweight and the projectile. Since I is a sum, the moment of inertia of each part can be calculated separately and then values can be added together to get the moment of inertia of the whole trebuchet arm. This makes calculating I much easier. The first part is the arm. It is like a rod with a certain mass per metre, m, and a certain length, l. The pivot is h metres from the centre of gravity of the arm. The diagram below illustrates this. In these conditions the following formula is true:
the sum of this for all the points. Luckily there is an easier way to go about it. The trebuchet arm is essentially made up of three different parts - the arm, the counterweight and the projectile. Since I is a sum, the moment of inertia of each part can be calculated separately and then values can be added together to get the moment of inertia of the whole trebuchet arm. This makes calculating I much easier. The first part is the arm. It is like a rod with a certain mass per metre, m, and a certain length, l. The pivot is h metres from the centre of gravity of the arm. The diagram below illustrates this. In these conditions the following formula is true:
Iarm=ml2/12+mh2

For simplicity I am assuming that the counterweight and the projectile are point masses and that their entire weight is at one point at the end of the arm. This means there is only one point to calculate I for.
Iprojectile=mprojectile×lprojectile arm2
Icounterweight=mcounterweight×lcounterweight arm2
The last thing left is the sum of the forces. Each force is straight down, because it is due to gravity. These must be broken down into two forces: One perpendicular and one parallel to the trebuchet arm.
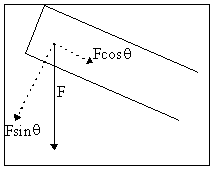 There are 4 forces in all acting on the trebuchet arm (ignoring friction for simplicity) and the same must be done for all four. The perpendicular force is the one which does the work and the parallel force is wasted, pushing down the trebuchet arm, trying to make the trebuchet fall over. This is countered by the trebuchet support frame, the fulcrum. The value of the perpendicular force in function of the downwards force is
There are 4 forces in all acting on the trebuchet arm (ignoring friction for simplicity) and the same must be done for all four. The perpendicular force is the one which does the work and the parallel force is wasted, pushing down the trebuchet arm, trying to make the trebuchet fall over. This is countered by the trebuchet support frame, the fulcrum. The value of the perpendicular force in function of the downwards force is  .
. 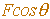 is wasted. The effect of
is wasted. The effect of 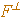 on the trebuchet depends on the distance from its point of application to the axis of rotation.
on the trebuchet depends on the distance from its point of application to the axis of rotation. 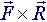 in the acceleration equation means the sum of all the
in the acceleration equation means the sum of all the 
 or
or  acting on the trebuchet. This shows us that the acceleration depends on the angle of the trebuchet arm.
acting on the trebuchet. This shows us that the acceleration depends on the angle of the trebuchet arm.

The closer the arm to parallel to the ground, the closer  is to 90 so the more efficient the force
is to 90 so the more efficient the force 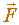 . Similarly, the greater the distance of application from the centre of rotation the more efficient the force is.
. Similarly, the greater the distance of application from the centre of rotation the more efficient the force is.
BackNextHome
© Filip Radlinski 1996, 1997

 . This is for a mathematical point motion but a similar formula is used for rotational rigid body motion.
. This is for a mathematical point motion but a similar formula is used for rotational rigid body motion.
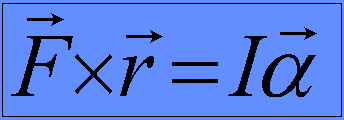 This formula is the shown on the right.
This formula is the shown on the right.  is acceleration but of the rotational type. It is called angular acceleration and is measured in radians per second squared. I is a function of the mass yet calculating it is slightly more complicated than calculating the total mass with translation motion. The exact formula is shown below. The name for I is moment of inertia. The given formula means that you cut whatever is accelerating into an infinite number of points, calculate the mass of each one multiplied by the distance from this point to the centre of rotation squared, and take
is acceleration but of the rotational type. It is called angular acceleration and is measured in radians per second squared. I is a function of the mass yet calculating it is slightly more complicated than calculating the total mass with translation motion. The exact formula is shown below. The name for I is moment of inertia. The given formula means that you cut whatever is accelerating into an infinite number of points, calculate the mass of each one multiplied by the distance from this point to the centre of rotation squared, and take  the sum of this for all the points. Luckily there is an easier way to go about it. The trebuchet arm is essentially made up of three different parts - the arm, the counterweight and the projectile. Since I is a sum, the moment of inertia of each part can be calculated separately and then values can be added together to get the moment of inertia of the whole trebuchet arm. This makes calculating I much easier. The first part is the arm. It is like a rod with a certain mass per metre, m, and a certain length, l. The pivot is h metres from the centre of gravity of the arm. The diagram below illustrates this. In these conditions the following formula is true:
the sum of this for all the points. Luckily there is an easier way to go about it. The trebuchet arm is essentially made up of three different parts - the arm, the counterweight and the projectile. Since I is a sum, the moment of inertia of each part can be calculated separately and then values can be added together to get the moment of inertia of the whole trebuchet arm. This makes calculating I much easier. The first part is the arm. It is like a rod with a certain mass per metre, m, and a certain length, l. The pivot is h metres from the centre of gravity of the arm. The diagram below illustrates this. In these conditions the following formula is true:
 There are 4 forces in all acting on the trebuchet arm (ignoring friction for simplicity) and the same must be done for all four. The perpendicular force is the one which does the work and the parallel force is wasted, pushing down the trebuchet arm, trying to make the trebuchet fall over. This is countered by the trebuchet support frame, the fulcrum. The value of the perpendicular force in function of the downwards force is
There are 4 forces in all acting on the trebuchet arm (ignoring friction for simplicity) and the same must be done for all four. The perpendicular force is the one which does the work and the parallel force is wasted, pushing down the trebuchet arm, trying to make the trebuchet fall over. This is countered by the trebuchet support frame, the fulcrum. The value of the perpendicular force in function of the downwards force is  .
. 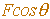 is wasted. The effect of
is wasted. The effect of 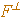 on the trebuchet depends on the distance from its point of application to the axis of rotation.
on the trebuchet depends on the distance from its point of application to the axis of rotation. 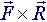 in the acceleration equation means the sum of all the
in the acceleration equation means the sum of all the 
 or
or  acting on the trebuchet. This shows us that the acceleration depends on the angle of the trebuchet arm.
acting on the trebuchet. This shows us that the acceleration depends on the angle of the trebuchet arm.
 is to 90 so the more efficient the force
is to 90 so the more efficient the force 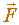 . Similarly, the greater the distance of application from the centre of rotation the more efficient the force is.
. Similarly, the greater the distance of application from the centre of rotation the more efficient the force is.